Base class for all dense matrices, vectors, and arrays. More...
#include <DenseBase.h>
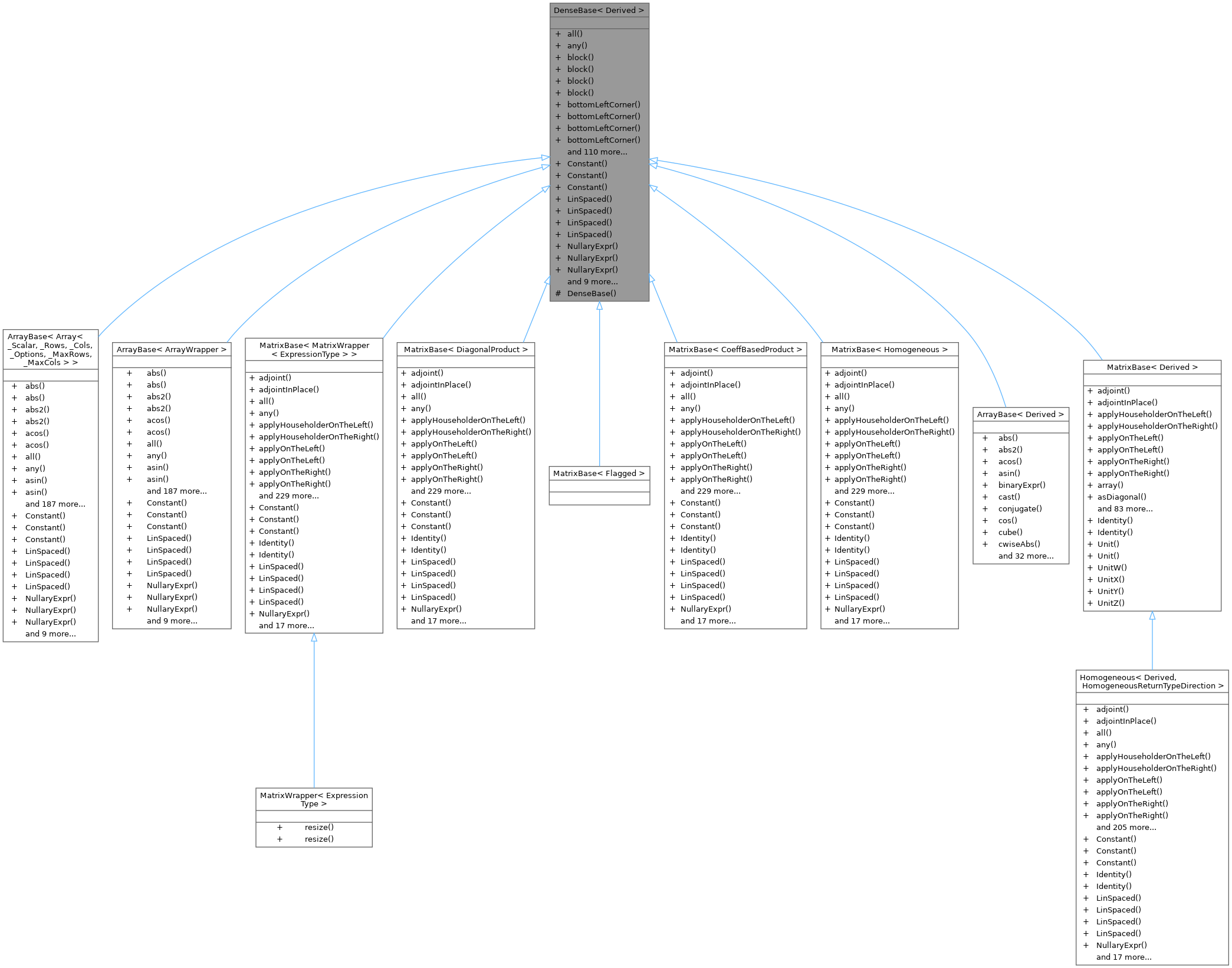
Inheritance diagram for DenseBase< Derived >:Public Types | |
| enum | { RowsAtCompileTime , ColsAtCompileTime , SizeAtCompileTime , MaxRowsAtCompileTime , MaxColsAtCompileTime , MaxSizeAtCompileTime , IsVectorAtCompileTime , Flags , IsRowMajor , InnerSizeAtCompileTime , CoeffReadCost , InnerStrideAtCompileTime , OuterStrideAtCompileTime } |
| typedef internal::traits< Derived >::Index | Index |
| The type of indices. | |
Public Member Functions | |
| bool | all (void) const |
| bool | any (void) const |
| template<int BlockRows, int BlockCols> | |
| Block< Derived, BlockRows, BlockCols > | block (Index startRow, Index startCol) |
| template<int BlockRows, int BlockCols> | |
| const Block< const Derived, BlockRows, BlockCols > | block (Index startRow, Index startCol) const |
| Block< Derived > | block (Index startRow, Index startCol, Index blockRows, Index blockCols) |
| const Block< const Derived > | block (Index startRow, Index startCol, Index blockRows, Index blockCols) const |
| template<int CRows, int CCols> | |
| Block< Derived, CRows, CCols > | bottomLeftCorner () |
| template<int CRows, int CCols> | |
| const Block< const Derived, CRows, CCols > | bottomLeftCorner () const |
| Block< Derived > | bottomLeftCorner (Index cRows, Index cCols) |
| const Block< const Derived > | bottomLeftCorner (Index cRows, Index cCols) const |
| template<int CRows, int CCols> | |
| Block< Derived, CRows, CCols > | bottomRightCorner () |
| template<int CRows, int CCols> | |
| const Block< const Derived, CRows, CCols > | bottomRightCorner () const |
| Block< Derived > | bottomRightCorner (Index cRows, Index cCols) |
| const Block< const Derived > | bottomRightCorner (Index cRows, Index cCols) const |
| template<int N> | |
| NRowsBlockXpr< N >::Type | bottomRows () |
| template<int N> | |
| ConstNRowsBlockXpr< N >::Type | bottomRows () const |
| RowsBlockXpr | bottomRows (Index n) |
| ConstRowsBlockXpr | bottomRows (Index n) const |
| ColXpr | col (Index i) |
| ConstColXpr | col (Index i) const |
| ColwiseReturnType | colwise () |
| ConstColwiseReturnType | colwise () const |
| Index | count () const |
| EvalReturnType | eval () const |
| void | fill (const Scalar &value) |
| template<unsigned int Added, unsigned int Removed> | |
| const Flagged< Derived, Added, Removed > | flagged () const |
| const WithFormat< Derived > | format (const IOFormat &fmt) const |
| template<int Size> | |
| DenseBase< Derived >::template FixedSegmentReturnType< Size >::Type | head () |
| template<int Size> | |
| DenseBase< Derived >::template ConstFixedSegmentReturnType< Size >::Type | head () const |
| SegmentReturnType | head (Index size) |
| DenseBase::ConstSegmentReturnType | head (Index size) const |
| Index | innerSize () const |
| template<typename OtherDerived> | |
| bool | isApprox (const DenseBase< OtherDerived > &other, RealScalar prec=NumTraits< Scalar >::dummy_precision()) const |
| bool | isApproxToConstant (const Scalar &value, RealScalar prec=NumTraits< Scalar >::dummy_precision()) const |
| bool | isConstant (const Scalar &value, RealScalar prec=NumTraits< Scalar >::dummy_precision()) const |
| template<typename OtherDerived> | |
| bool | isMuchSmallerThan (const DenseBase< OtherDerived > &other, RealScalar prec=NumTraits< Scalar >::dummy_precision()) const |
| template<typename Derived> | |
| bool | isMuchSmallerThan (const typename NumTraits< Scalar >::Real &other, RealScalar prec) const |
| bool | isOnes (RealScalar prec=NumTraits< Scalar >::dummy_precision()) const |
| bool | isZero (RealScalar prec=NumTraits< Scalar >::dummy_precision()) const |
| template<int N> | |
| NColsBlockXpr< N >::Type | leftCols () |
| template<int N> | |
| ConstNColsBlockXpr< N >::Type | leftCols () const |
| ColsBlockXpr | leftCols (Index n) |
| ConstColsBlockXpr | leftCols (Index n) const |
| internal::traits< Derived >::Scalar | maxCoeff () const |
| template<typename IndexType> | |
| internal::traits< Derived >::Scalar | maxCoeff (IndexType *index) const |
| template<typename IndexType> | |
| internal::traits< Derived >::Scalar | maxCoeff (IndexType *row, IndexType *col) const |
| Scalar | mean () const |
| template<int N> | |
| NColsBlockXpr< N >::Type | middleCols (Index startCol) |
| template<int N> | |
| ConstNColsBlockXpr< N >::Type | middleCols (Index startCol) const |
| ColsBlockXpr | middleCols (Index startCol, Index numCols) |
| ConstColsBlockXpr | middleCols (Index startCol, Index numCols) const |
| template<int N> | |
| NRowsBlockXpr< N >::Type | middleRows (Index startRow) |
| template<int N> | |
| ConstNRowsBlockXpr< N >::Type | middleRows (Index startRow) const |
| RowsBlockXpr | middleRows (Index startRow, Index numRows) |
| ConstRowsBlockXpr | middleRows (Index startRow, Index numRows) const |
| internal::traits< Derived >::Scalar | minCoeff () const |
| template<typename IndexType> | |
| internal::traits< Derived >::Scalar | minCoeff (IndexType *index) const |
| template<typename IndexType> | |
| internal::traits< Derived >::Scalar | minCoeff (IndexType *row, IndexType *col) const |
| const NestByValue< Derived > | nestByValue () const |
| Index | nonZeros () const |
| template<typename OtherDerived> | |
| CommaInitializer< Derived > | operator<< (const DenseBase< OtherDerived > &other) |
| CommaInitializer< Derived > | operator<< (const Scalar &s) |
| Derived & | operator= (const DenseBase &other) |
| template<typename OtherDerived> | |
| Derived & | operator= (const DenseBase< OtherDerived > &other) |
| template<typename OtherDerived> | |
| Derived & | operator= (const EigenBase< OtherDerived > &other) |
| Copies the generic expression other into *this. | |
| Index | outerSize () const |
| Scalar | prod () const |
| template<typename Func> | |
| internal::result_of< Func(typenameinternal::traits< Derived >::Scalar)>::type | redux (const Func &func) const |
| template<int RowFactor, int ColFactor> | |
| const Replicate< Derived, RowFactor, ColFactor > | replicate () const |
| const Replicate< Derived, Dynamic, Dynamic > | replicate (Index rowFacor, Index colFactor) const |
| void | resize (Index rows, Index cols) |
| void | resize (Index size) |
| ReverseReturnType | reverse () |
| ConstReverseReturnType | reverse () const |
| void | reverseInPlace () |
| template<int N> | |
| NColsBlockXpr< N >::Type | rightCols () |
| template<int N> | |
| ConstNColsBlockXpr< N >::Type | rightCols () const |
| ColsBlockXpr | rightCols (Index n) |
| ConstColsBlockXpr | rightCols (Index n) const |
| RowXpr | row (Index i) |
| ConstRowXpr | row (Index i) const |
| RowwiseReturnType | rowwise () |
| ConstRowwiseReturnType | rowwise () const |
| template<int Size> | |
| DenseBase< Derived >::template FixedSegmentReturnType< Size >::Type | segment (Index start) |
| template<int Size> | |
| DenseBase< Derived >::template ConstFixedSegmentReturnType< Size >::Type | segment (Index start) const |
| SegmentReturnType | segment (Index start, Index size) |
| DenseBase::ConstSegmentReturnType | segment (Index start, Index size) const |
| template<typename ThenDerived, typename ElseDerived> | |
| const Select< Derived, ThenDerived, ElseDerived > | select (const DenseBase< ThenDerived > &thenMatrix, const DenseBase< ElseDerived > &elseMatrix) const |
| template<typename ThenDerived> | |
| const Select< Derived, ThenDerived, typename ThenDerived::ConstantReturnType > | select (const DenseBase< ThenDerived > &thenMatrix, typename ThenDerived::Scalar elseScalar) const |
| template<typename ElseDerived> | |
| const Select< Derived, typename ElseDerived::ConstantReturnType, ElseDerived > | select (typename ElseDerived::Scalar thenScalar, const DenseBase< ElseDerived > &elseMatrix) const |
| Derived & | setConstant (const Scalar &value) |
| Derived & | setLinSpaced (const Scalar &low, const Scalar &high) |
| Sets a linearly space vector. | |
| Derived & | setLinSpaced (Index size, const Scalar &low, const Scalar &high) |
| Sets a linearly space vector. | |
| Derived & | setOnes () |
| Derived & | setRandom () |
| Derived & | setZero () |
| Scalar | sum () const |
| template<typename OtherDerived> | |
| void | swap (const DenseBase< OtherDerived > &other, int=OtherDerived::ThisConstantIsPrivateInPlainObjectBase) |
| template<typename OtherDerived> | |
| void | swap (PlainObjectBase< OtherDerived > &other) |
| template<int Size> | |
| DenseBase< Derived >::template FixedSegmentReturnType< Size >::Type | tail () |
| template<int Size> | |
| DenseBase< Derived >::template ConstFixedSegmentReturnType< Size >::Type | tail () const |
| SegmentReturnType | tail (Index size) |
| DenseBase::ConstSegmentReturnType | tail (Index size) const |
| template<int CRows, int CCols> | |
| Block< Derived, CRows, CCols > | topLeftCorner () |
| template<int CRows, int CCols> | |
| const Block< const Derived, CRows, CCols > | topLeftCorner () const |
| Block< Derived > | topLeftCorner (Index cRows, Index cCols) |
| const Block< const Derived > | topLeftCorner (Index cRows, Index cCols) const |
| template<int CRows, int CCols> | |
| Block< Derived, CRows, CCols > | topRightCorner () |
| template<int CRows, int CCols> | |
| const Block< const Derived, CRows, CCols > | topRightCorner () const |
| Block< Derived > | topRightCorner (Index cRows, Index cCols) |
| const Block< const Derived > | topRightCorner (Index cRows, Index cCols) const |
| template<int N> | |
| NRowsBlockXpr< N >::Type | topRows () |
| template<int N> | |
| ConstNRowsBlockXpr< N >::Type | topRows () const |
| RowsBlockXpr | topRows (Index n) |
| ConstRowsBlockXpr | topRows (Index n) const |
| Eigen::Transpose< Derived > | transpose () |
| ConstTransposeReturnType | transpose () const |
| void | transposeInPlace () |
| CoeffReturnType | value () const |
| template<typename Visitor> | |
| void | visit (Visitor &func) const |
Static Public Member Functions | |
| static const ConstantReturnType | Constant (const Scalar &value) |
| static const ConstantReturnType | Constant (Index rows, Index cols, const Scalar &value) |
| static const ConstantReturnType | Constant (Index size, const Scalar &value) |
| static const RandomAccessLinSpacedReturnType | LinSpaced (const Scalar &low, const Scalar &high) |
| Sets a linearly space vector. | |
| static const RandomAccessLinSpacedReturnType | LinSpaced (Index size, const Scalar &low, const Scalar &high) |
| Sets a linearly space vector. | |
| static const SequentialLinSpacedReturnType | LinSpaced (Sequential_t, const Scalar &low, const Scalar &high) |
| Sets a linearly space vector. | |
| static const SequentialLinSpacedReturnType | LinSpaced (Sequential_t, Index size, const Scalar &low, const Scalar &high) |
| Sets a linearly space vector. | |
| template<typename CustomNullaryOp> | |
| static const CwiseNullaryOp< CustomNullaryOp, Derived > | NullaryExpr (const CustomNullaryOp &func) |
| template<typename CustomNullaryOp> | |
| static const CwiseNullaryOp< CustomNullaryOp, Derived > | NullaryExpr (Index rows, Index cols, const CustomNullaryOp &func) |
| template<typename CustomNullaryOp> | |
| static const CwiseNullaryOp< CustomNullaryOp, Derived > | NullaryExpr (Index size, const CustomNullaryOp &func) |
| static const ConstantReturnType | Ones () |
| static const ConstantReturnType | Ones (Index rows, Index cols) |
| static const ConstantReturnType | Ones (Index size) |
| static const CwiseNullaryOp< internal::scalar_random_op< Scalar >, Derived > | Random () |
| static const CwiseNullaryOp< internal::scalar_random_op< Scalar >, Derived > | Random (Index rows, Index cols) |
| static const CwiseNullaryOp< internal::scalar_random_op< Scalar >, Derived > | Random (Index size) |
| static const ConstantReturnType | Zero () |
| static const ConstantReturnType | Zero (Index rows, Index cols) |
| static const ConstantReturnType | Zero (Index size) |
Protected Member Functions | |
| DenseBase () | |
Related Symbols | |
(Note that these are not member symbols.) | |
| template<typename Derived> | |
| std::ostream & | operator<< (std::ostream &s, const DenseBase< Derived > &m) |
Base class for all dense matrices, vectors, and arrays.
This class is the base that is inherited by all dense objects (matrix, vector, arrays, and related expression types). The common Eigen API for dense objects is contained in this class.
| Derived | is the derived type, e.g., a matrix type or an expression. |
This class can be extended with the help of the plugin mechanism described on the page Customizing/Extending Eigen by defining the preprocessor symbol EIGEN_DENSEBASE_PLUGIN.
| typedef internal::traits<Derived>::Index Index |
The type of indices.
To change this, #define the preprocessor symbol EIGEN_DEFAULT_DENSE_INDEX_TYPE.
| anonymous enum |
| Enumerator | |
|---|---|
| RowsAtCompileTime | The number of rows at compile-time. This is just a copy of the value provided by the Derived type. If a value is not known at compile-time, it is set to the Dynamic constant.
|
| ColsAtCompileTime | The number of columns at compile-time. This is just a copy of the value provided by the Derived type. If a value is not known at compile-time, it is set to the Dynamic constant.
|
| SizeAtCompileTime | This is equal to the number of coefficients, i.e. the number of rows times the number of columns, or to Dynamic if this is not known at compile-time.
|
| MaxRowsAtCompileTime | This value is equal to the maximum possible number of rows that this expression might have. If this expression might have an arbitrarily high number of rows, this value is set to Dynamic. This value is useful to know when evaluating an expression, in order to determine whether it is possible to avoid doing a dynamic memory allocation. |
| MaxColsAtCompileTime | This value is equal to the maximum possible number of columns that this expression might have. If this expression might have an arbitrarily high number of columns, this value is set to Dynamic. This value is useful to know when evaluating an expression, in order to determine whether it is possible to avoid doing a dynamic memory allocation. |
| MaxSizeAtCompileTime | This value is equal to the maximum possible number of coefficients that this expression might have. If this expression might have an arbitrarily high number of coefficients, this value is set to Dynamic. This value is useful to know when evaluating an expression, in order to determine whether it is possible to avoid doing a dynamic memory allocation. |
| IsVectorAtCompileTime | This is set to true if either the number of rows or the number of columns is known at compile-time to be equal to 1. Indeed, in that case, we are dealing with a column-vector (if there is only one column) or with a row-vector (if there is only one row). |
| Flags | This stores expression Flags flags which may or may not be inherited by new expressions constructed from this one. See the list of flags. |
| IsRowMajor | True if this expression has row-major storage order. |
| CoeffReadCost | This is a rough measure of how expensive it is to read one coefficient from this expression. |
|
inlineprotected |
Default constructor. Do nothing.
References IsRowMajor, MaxColsAtCompileTime, and MaxRowsAtCompileTime.
Referenced by bottomLeftCorner(), bottomLeftCorner(), ArrayBase< Array< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols > >::cwiseInverse(), MatrixBase< MatrixWrapper< ExpressionType > >::cwiseInverse(), isApprox(), MatrixBase< MatrixWrapper< ExpressionType > >::isIdentity(), isMuchSmallerThan(), middleRows(), middleRows(), operator=(), operator=(), MatrixBase< MatrixWrapper< ExpressionType > >::operator=(), rightCols(), rightCols(), select(), select(), select(), swap(), topRows(), topRows(), and MatrixBase< MatrixWrapper< ExpressionType > >::UnitY().
|
inline |
Example:
Output:
Is ( 0.68 -0.211 0.566) inside the box: 0 Is (0.597 0.823 0.605) inside the box: 1
References CoeffReadCost, and SizeAtCompileTime.
Referenced by rightCols().
|
inline |
References CoeffReadCost, and SizeAtCompileTime.
Referenced by rightCols().
|
inline |
The template parameters BlockRows and BlockCols are the number of rows and columns in the block.
| startRow | the first row in the block |
| startCol | the first column in the block |
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.block<2,2>(1,1): -6 1 -3 0 Now the matrix m is: 7 9 -5 -3 -2 0 0 0 6 0 0 9 6 6 3 9
|
inline |
This is the const version of block<>(Index, Index).
|
inline |
| startRow | the first row in the block |
| startCol | the first column in the block |
| blockRows | the number of rows in the block |
| blockCols | the number of columns in the block |
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.block(1, 1, 2, 2): -6 1 -3 0 Now the matrix m is: 7 9 -5 -3 -2 0 0 0 6 0 0 9 6 6 3 9
|
inline |
This is the const version of block(Index,Index,Index,Index).
|
inline |
The template parameters CRows and CCols are the number of rows and columns in the corner.
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.bottomLeftCorner<2,2>(): 6 -3 6 6 Now the matrix m is: 7 9 -5 -3 -2 -6 1 0 0 0 0 9 0 0 3 9
References DenseBase().
|
inline |
This is the const version of bottomLeftCorner<int, int>().
References DenseBase().
| cRows | the number of rows in the corner |
| cCols | the number of columns in the corner |
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.bottomLeftCorner(2, 2): 6 -3 6 6 Now the matrix m is: 7 9 -5 -3 -2 -6 1 0 0 0 0 9 0 0 3 9
|
inline |
This is the const version of bottomLeftCorner(Index, Index).
|
inline |
The template parameters CRows and CCols are the number of rows and columns in the corner.
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.bottomRightCorner<2,2>(): 0 9 3 9 Now the matrix m is: 7 9 -5 -3 -2 -6 1 0 6 -3 0 0 6 6 0 0
|
inline |
This is the const version of bottomRightCorner<int, int>().
References IsRowMajor, and IsVectorAtCompileTime.
| cRows | the number of rows in the corner |
| cCols | the number of columns in the corner |
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.bottomRightCorner(2, 2): 0 9 3 9 Now the matrix m is: 7 9 -5 -3 -2 -6 1 0 6 -3 0 0 6 6 0 0
|
inline |
This is the const version of bottomRightCorner(Index, Index).
|
inline |
| N | the number of rows in the block |
Example:
Output:
Here is the array a: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is a.bottomRows<2>(): 6 -3 0 9 6 6 3 9 Now the array a is: 7 9 -5 -3 -2 -6 1 0 0 0 0 0 0 0 0 0
|
inline |
This is the const version of bottomRows<int>().
References value().
|
inline |
| n | the number of rows in the block |
Example:
Output:
Here is the array a: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is a.bottomRows(2): 6 -3 0 9 6 6 3 9 Now the array a is: 7 9 -5 -3 -2 -6 1 0 0 0 0 0 0 0 0 0
References tail().
|
inline |
This is the const version of bottomRows(Index).
References value().
|
inline |
Example:
Output:
1 4 0 0 5 0 0 6 1
Referenced by MatrixBase< Derived >::applyHouseholderOnTheRight(), MatrixBase< Derived >::applyOnTheRight(), VectorwiseOp< ExpressionType, Direction >::cross(), leftCols(), maxCoeff(), and minCoeff().
|
inline |
This is the const version of col().
|
inline |
References colwise().
|
inline |
Example:
Output:
Here is the matrix m: 0.68 0.597 -0.33 -0.211 0.823 0.536 0.566 -0.605 -0.444 Here is the sum of each column: 1.04 0.815 -0.238 Here is the maximum absolute value of each column: 0.68 0.823 0.536
References colwise().
Referenced by colwise(), colwise(), rightCols(), and Eigen::umeyama().
|
inlinestatic |
This variant is only for fixed-size DenseBase types. For dynamic-size types, you need to use the variants taking size arguments.
The template parameter CustomNullaryOp is the type of the functor.
References ColsAtCompileTime, NullaryExpr(), RowsAtCompileTime, and value().
|
inlinestatic |
The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this DenseBase type.
This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Zero() should be used instead.
The template parameter CustomNullaryOp is the type of the functor.
References NullaryExpr(), and value().
Referenced by Ones(), Ones(), Ones(), Zero(), Zero(), and Zero().
|
inlinestatic |
The parameter size is the size of the returned vector. Must be compatible with this DenseBase type.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Zero() should be used instead.
The template parameter CustomNullaryOp is the type of the functor.
References NullaryExpr(), and value().
Referenced by rightCols().
|
inline |
Notice that in the case of a plain matrix or vector (not an expression) this function just returns a const reference, in order to avoid a useless copy.
Referenced by MatrixBase< Derived >::colPivHouseholderQr(), MatrixBase< Derived >::fullPivHouseholderQr(), MatrixBase< Derived >::fullPivLu(), MatrixBase< Derived >::householderQr(), MatrixBase< Derived >::lu(), and MatrixBase< Derived >::partialPivLu().
|
inline |
Alias for setConstant(): sets all coefficients in this expression to value.
References setConstant(), and value().
|
inline |
This is mostly for internal use.
|
inline |
See class IOFormat for some examples.
|
inline |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
The template parameter Size is the number of coefficients in the block
Example:
Output:
Here is the vector v: 7 -2 6 6 Here is v.head(2): 7 -2 Now the vector v is: 0 0 6 6
|
inline |
This is the const version of head<int>().
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
| size | the number of coefficients in the block |
Example:
Output:
Here is the vector v: 7 -2 6 6 Here is v.head(2): 7 -2 Now the vector v is: 0 0 6 6
References head().
Referenced by head(), head(), DenseBase< ArrayWrapper< ExpressionType > >::head(), DenseBase< ArrayWrapper< ExpressionType > >::head(), and MatrixBase< Derived >::stableNorm().
|
inline |
This is the const version of head(Index).
References head().
|
inline |
| bool isApprox | ( | const DenseBase< OtherDerived > & | other, |
| RealScalar | prec = NumTraits<Scalar>::dummy_precision() ) const |
true if *this is approximately equal to other, within the precision determined by prec.
![\[ \Vert v - w \Vert \leqslant p\,\min(\Vert v\Vert, \Vert w\Vert). \]](form_15_dark.png)
*this is approximately equal to the zero matrix or vector. Indeed, isApprox(zero) returns false unless *this itself is exactly the zero matrix or vector. If you want to test whether *this is zero, use internal::isMuchSmallerThan(const
RealScalar&, RealScalar) instead.References DenseBase().
| bool isApproxToConstant | ( | const Scalar & | value, |
| RealScalar | prec = NumTraits<Scalar>::dummy_precision() ) const |
| bool isConstant | ( | const Scalar & | value, |
| RealScalar | prec = NumTraits<Scalar>::dummy_precision() ) const |
This is just an alias for isApproxToConstant().
| bool isMuchSmallerThan | ( | const DenseBase< OtherDerived > & | other, |
| RealScalar | prec = NumTraits<Scalar>::dummy_precision() ) const |
true if the norm of *this is much smaller than the norm of other, within the precision determined by prec.
![\[ \Vert v \Vert \leqslant p\,\Vert w\Vert. \]](form_18_dark.png)
References DenseBase().
| bool isMuchSmallerThan | ( | const typename NumTraits< Scalar >::Real & | other, |
| RealScalar | prec ) const |
true if the norm of *this is much smaller than other, within the precision determined by prec.
![\[ \Vert v \Vert \leqslant p\,\vert x\vert. \]](form_17_dark.png)
For matrices, the comparison is done using the Hilbert-Schmidt norm. For this reason, the value of the reference scalar other should come from the Hilbert-Schmidt norm of a reference matrix of same dimensions.
| bool isOnes | ( | RealScalar | prec = NumTraits<Scalar>::dummy_precision() | ) | const |
Example:
Output:
Here's the matrix m: 1 1 1 1 1 1 1 1 1 m.isOnes() returns: 0 m.isOnes(1e-3) returns: 1
References isApproxToConstant().
| bool isZero | ( | RealScalar | prec = NumTraits<Scalar>::dummy_precision() | ) | const |
Example:
Output:
Here's the matrix m:
0 0 0.0001
0 0 0
0 0 0
m.isZero() returns: 0
m.isZero(1e-3) returns: 1
|
inline |
| N | the number of columns in the block |
Example:
Output:
Here is the array a: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is a.leftCols<2>(): 7 9 -2 -6 6 -3 6 6 Now the array a is: 0 0 -5 -3 0 0 1 0 0 0 0 9 0 0 3 9
|
inline |
This is the const version of leftCols<int>().
|
inline |
| n | the number of columns in the block |
Example:
Output:
Here is the array a: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is a.leftCols(2): 7 9 -2 -6 6 -3 6 6 Now the array a is: 0 0 -5 -3 0 0 1 0 0 0 0 9 0 0 3 9
|
inline |
This is the const version of leftCols(Index).
|
inlinestatic |
Sets a linearly space vector.
The function generates 'size' equally spaced values in the closed interval [low,high]. When size is set to 1, a vector of length 1 containing 'high' is returned.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
Example:
Output:
7 8 9 10 0 0.25 0.5 0.75 1
References NullaryExpr().
|
inlinestatic |
Sets a linearly space vector.
The function generates 'size' equally spaced values in the closed interval [low,high]. When size is set to 1, a vector of length 1 containing 'high' is returned.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
Example:
Output:
7 8 9 10 0 0.25 0.5 0.75 1
References NullaryExpr().
|
inlinestatic |
Sets a linearly space vector.
The function generates 'size' equally spaced values in the closed interval [low,high]. This particular version of LinSpaced() uses sequential access, i.e. vector access is assumed to be a(0), a(1), ..., a(size). This assumption allows for better vectorization and yields faster code than the random access version.
When size is set to 1, a vector of length 1 containing 'high' is returned.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
Example:
Output:
7 8 9 10 0 0.25 0.5 0.75 1
|
inlinestatic |
Sets a linearly space vector.
The function generates 'size' equally spaced values in the closed interval [low,high]. This particular version of LinSpaced() uses sequential access, i.e. vector access is assumed to be a(0), a(1), ..., a(size). This assumption allows for better vectorization and yields faster code than the random access version.
When size is set to 1, a vector of length 1 containing 'high' is returned.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
Example:
Output:
7 8 9 10 0 0.25 0.5 0.75 1
References NullaryExpr().
|
inline |
| internal::traits< Derived >::Scalar maxCoeff | ( | IndexType * | index | ) | const |
References RowsAtCompileTime, and visit().
| internal::traits< Derived >::Scalar maxCoeff | ( | IndexType * | row, |
| IndexType * | col ) const |
|
inline |
|
inline |
| N | the number of columns in the block |
| startCol | the index of the first column in the block |
Example:
Output:
A = 7 -6 0 9 -10 -2 -3 3 3 -5 6 6 -3 5 -8 6 -5 0 -8 6 9 1 9 2 -7 A(:,1..3) = -6 0 9 -3 3 3 6 -3 5 -5 0 -8 1 9 2
|
inline |
This is the const version of middleCols<int>().
| startCol | the index of the first column in the block |
| numCols | the number of columns in the block |
Example:
Output:
A = 7 -6 0 9 -10 -2 -3 3 3 -5 6 6 -3 5 -8 6 -5 0 -8 6 9 1 9 2 -7 A(1..3,:) = -6 0 9 -3 3 3 6 -3 5 -5 0 -8 1 9 2
References reverse(), and reverseInPlace().
|
inline |
This is the const version of middleCols(Index,Index).
|
inline |
| N | the number of rows in the block |
| startRow | the index of the first row in the block |
Example:
Output:
A = 7 -6 0 9 -10 -2 -3 3 3 -5 6 6 -3 5 -8 6 -5 0 -8 6 9 1 9 2 -7 A(1..3,:) = -2 -3 3 3 -5 6 6 -3 5 -8 6 -5 0 -8 6
|
inline |
This is the const version of middleRows<int>().
| startRow | the index of the first row in the block |
| numRows | the number of rows in the block |
Example:
Output:
A = 7 -6 0 9 -10 -2 -3 3 3 -5 6 6 -3 5 -8 6 -5 0 -8 6 9 1 9 2 -7 A(2..3,:) = 6 6 -3 5 -8 6 -5 0 -8 6
References DenseBase().
|
inline |
This is the const version of middleRows(Index,Index).
References DenseBase(), and value().
|
inline |
| internal::traits< Derived >::Scalar minCoeff | ( | IndexType * | index | ) | const |
References RowsAtCompileTime, and visit().
| internal::traits< Derived >::Scalar minCoeff | ( | IndexType * | row, |
| IndexType * | col ) const |
|
inline |
|
inline |
|
inlinestatic |
This variant is only for fixed-size DenseBase types. For dynamic-size types, you need to use the variants taking size arguments.
The template parameter CustomNullaryOp is the type of the functor.
References ColsAtCompileTime, and RowsAtCompileTime.
|
inlinestatic |
The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.
This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Zero() should be used instead.
The template parameter CustomNullaryOp is the type of the functor.
Referenced by Constant(), Constant(), Constant(), MatrixBase< Derived >::Identity(), MatrixBase< Derived >::Identity(), LinSpaced(), LinSpaced(), LinSpaced(), Random(), Random(), Random(), and MatrixBase< MatrixWrapper< ExpressionType > >::UnitW().
|
inlinestatic |
The parameter size is the size of the returned vector. Must be compatible with this MatrixBase type.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Zero() should be used instead.
The template parameter CustomNullaryOp is the type of the functor.
References RowsAtCompileTime.
|
inlinestatic |
This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variants taking size arguments.
Example:
Output:
1 1 1 1 6 6 6 6
References Constant().
|
inlinestatic |
The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.
This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Ones() should be used instead.
Example:
Output:
1 1 1 1 1 1
References Constant().
|
inlinestatic |
The parameter size is the size of the returned vector. Must be compatible with this MatrixBase type.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Ones() should be used instead.
Example:
Output:
6 6 6 6 1 1
References Constant().
|
inline |
|
inline |
Convenient operator to set the coefficients of a matrix.
The coefficients must be provided in a row major order and exactly match the size of the matrix. Otherwise an assertion is raised.
Example:
Output:
1 2 3 4 5 6 7 8 9 10 11 0 12 13 0 0 0 1 14 15 16 14 5 6 15 8 9
|
inline |
Special case of the template operator=, in order to prevent the compiler from generating a default operator= (issue hit with g++ 4.1)
References DenseBase().
|
inline |
| Derived & operator= | ( | const EigenBase< OtherDerived > & | other | ) |
Copies the generic expression other into *this.
The expression must provide a (templated) evalTo(Derived& dst) const function which does the actual job. In practice, this allows any user to write its own special matrix without having to modify MatrixBase
References EigenBase< Derived >::derived().
|
inline |
References IsRowMajor, and IsVectorAtCompileTime.
|
inline |
Example:
Output:
Here is the matrix m: 0.68 0.597 -0.33 -0.211 0.823 0.536 0.566 -0.605 -0.444 Here is the product of all the coefficients: 0.0019
References SizeAtCompileTime.
|
inlinestatic |
This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variants taking size arguments.
Example:
Output:
700 600 -200 600
This expression has the "evaluate before nesting" flag so that it will be evaluated into a temporary matrix whenever it is nested in a larger expression. This prevents unexpected behavior with expressions involving random matrices.
References ColsAtCompileTime, NullaryExpr(), and RowsAtCompileTime.
|
inlinestatic |
The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.
This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Random() should be used instead.
Example:
Output:
7 6 9 -2 6 -6
This expression has the "evaluate before nesting" flag so that it will be evaluated into a temporary matrix whenever it is nested in a larger expression. This prevents unexpected behavior with expressions involving random matrices.
References NullaryExpr().
Referenced by rightCols(), rightCols(), and setRandom().
|
inlinestatic |
The parameter size is the size of the returned vector. Must be compatible with this MatrixBase type.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Random() should be used instead.
Example:
Output:
7 -2
This expression has the "evaluate before nesting" flag so that it will be evaluated into a temporary vector whenever it is nested in a larger expression. This prevents unexpected behavior with expressions involving random matrices.
References NullaryExpr().
|
inline |
The template parameter BinaryOp is the type of the functor func which must be an associative operator. Both current STL and TR1 functor styles are handled.
|
inline |
*this Example:
Output:
Here is the matrix m: 7 6 9 -2 6 -6 m.replicate<3,2>() = ... 7 6 9 7 6 9 -2 6 -6 -2 6 -6 7 6 9 7 6 9 -2 6 -6 -2 6 -6 7 6 9 7 6 9 -2 6 -6 -2 6 -6
Referenced by rightCols().
|
inline |
*this Example:
Output:
Here is the vector v: 7 -2 6 v.replicate(2,5) = ... 7 7 7 7 7 -2 -2 -2 -2 -2 6 6 6 6 6 7 7 7 7 7 -2 -2 -2 -2 -2 6 6 6 6 6
Only plain matrices/arrays, not expressions, may be resized; therefore the only useful resize methods are Matrix::resize() and Array::resize(). The present method only asserts that the new size equals the old size, and does nothing else.
|
inline |
Only plain matrices/arrays, not expressions, may be resized; therefore the only useful resize methods are Matrix::resize() and Array::resize(). The present method only asserts that the new size equals the old size, and does nothing else.
|
inline |
Example:
Output:
Here is the matrix m: 7 6 -3 1 -2 9 6 0 6 -6 -5 3 Here is the reverse of m: 3 -5 -6 6 0 6 9 -2 1 -3 6 7 Here is the coefficient (1,0) in the reverse of m: 0 Let us overwrite this coefficient with the value 4. Now the matrix m is: 7 6 -3 1 -2 9 6 4 6 -6 -5 3
Referenced by middleCols().
|
inline |
This is the const version of reverse().
|
inline |
This is the "in place" version of reverse: it reverses *this.
In most cases it is probably better to simply use the reversed expression of a matrix. However, when reversing the matrix data itself is really needed, then this "in-place" version is probably the right choice because it provides the following additional features:
Referenced by middleCols().
|
inline |
| N | the number of columns in the block |
Example:
Output:
Here is the array a: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is a.rightCols<2>(): -5 -3 1 0 0 9 3 9 Now the array a is: 7 9 0 0 -2 -6 0 0 6 -3 0 0 6 6 0 0
References DenseBase(), Random(), and select().
|
inline |
This is the const version of rightCols<int>().
References Eigen::BothDirections, DenseBase(), replicate(), and select().
|
inline |
| n | the number of columns in the block |
Example:
Output:
Here is the array a: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is a.rightCols(2): -5 -3 1 0 0 9 3 9 Now the array a is: 7 9 0 0 -2 -6 0 0 6 -3 0 0 6 6 0 0
|
inline |
This is the const version of rightCols(Index).
References all(), any(), colwise(), count(), Eigen::Horizontal, Random(), rowwise(), and Eigen::Vertical.
|
inline |
Example:
Output:
1 0 0 4 5 6 0 0 1
Referenced by MatrixBase< Derived >::applyHouseholderOnTheLeft(), MatrixBase< Derived >::applyOnTheLeft(), VectorwiseOp< ExpressionType, Direction >::cross(), leftCols(), maxCoeff(), minCoeff(), Transform< Scalar, Dim, Mode, Options >::operator*, Translation< Scalar, Dim >::operator*, and Transform< Scalar, Dim, Mode, Options >::pretranslate().
|
inline |
This is the const version of row().
|
inline |
References rowwise().
|
inline |
Example:
Output:
Here is the matrix m: 0.68 0.597 -0.33 -0.211 0.823 0.536 0.566 -0.605 -0.444 Here is the sum of each row: 0.948 1.15 -0.483 Here is the maximum absolute value of each row: 0.68 0.823 0.605
References rowwise().
Referenced by rightCols(), rowwise(), rowwise(), and Eigen::umeyama().
|
inline |
*this This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
The template parameter Size is the number of coefficients in the block
| start | the index of the first element of the sub-vector |
Example:
Output:
Here is the vector v: 7 -2 6 6 Here is v.segment<2>(1): -2 6 Now the vector v is: 7 -2 0 0
|
inline |
This is the const version of segment<int>(Index).
|
inline |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
| start | the first coefficient in the segment |
| size | the number of coefficients in the segment |
Example:
Output:
Here is the vector v: 7 -2 6 6 Here is v.segment(1, 2): -2 6 Now the vector v is: 7 0 0 6
Referenced by MatrixBase< Derived >::stableNorm().
|
inline |
This is the const version of segment(Index,Index).
|
inline |
*this(i,j), and elseMatrix(i,j) otherwise.Example:
Output:
1 2 3 4 -5 -6 -7 -8 -9
References DenseBase().
Referenced by rightCols(), and rightCols().
|
inline |
Version of DenseBase::select(const DenseBase&, const DenseBase&) with the else expression being a scalar value.
References DenseBase().
|
inline |
Version of DenseBase::select(const DenseBase&, const DenseBase&) with the then expression being a scalar value.
References DenseBase().
|
inline |
Sets all coefficients in this expression to value.
|
inline |
Sets a linearly space vector.
The function fill *this with equally spaced values in the closed interval [low,high]. When size is set to 1, a vector of length 1 containing 'high' is returned.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
References setLinSpaced().
|
inline |
Sets a linearly space vector.
The function generates 'size' equally spaced values in the closed interval [low,high]. When size is set to 1, a vector of length 1 containing 'high' is returned.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
Example:
Output:
0.5 0.75 1 1.25 1.5
Referenced by setLinSpaced().
|
inline |
Sets all coefficients in this expression to one.
Example:
Output:
7 9 -5 -3 1 1 1 1 6 -3 0 9 6 6 3 9
References setConstant().
|
inline |
Sets all coefficients in this expression to random values.
Example:
Output:
0 7 0 0 0 -2 0 0 0 6 0 0 0 6 0 0
References Random().
|
inline |
Sets all coefficients in this expression to zero.
Example:
Output:
7 9 -5 -3 0 0 0 0 6 -3 0 9 6 6 3 9
References setConstant().
|
inline |
References SizeAtCompileTime.
|
inline |
swaps *this with the expression other.
References DenseBase().
|
inline |
swaps *this with the matrix or array other.
|
inline |
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
The template parameter Size is the number of coefficients in the block
Example:
Output:
Here is the vector v: 7 -2 6 6 Here is v.tail(2): 6 6 Now the vector v is: 7 -2 0 0
|
inline |
This is the const version of tail<int>.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
| size | the number of coefficients in the block |
Example:
Output:
Here is the vector v: 7 -2 6 6 Here is v.tail(2): 6 6 Now the vector v is: 7 -2 0 0
References tail().
Referenced by bottomRows(), MatrixBase< Derived >::makeHouseholder(), tail(), tail(), DenseBase< ArrayWrapper< ExpressionType > >::tail(), and DenseBase< ArrayWrapper< ExpressionType > >::tail().
|
inline |
This is the const version of tail(Index).
References tail().
|
inline |
The template parameters CRows and CCols are the number of rows and columns in the corner.
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.topLeftCorner<2,2>(): 7 9 -2 -6 Now the matrix m is: 0 0 -5 -3 0 0 1 0 6 -3 0 9 6 6 3 9
|
inline |
This is the const version of topLeftCorner<int, int>().
| cRows | the number of rows in the corner |
| cCols | the number of columns in the corner |
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.topLeftCorner(2, 2): 7 9 -2 -6 Now the matrix m is: 0 0 -5 -3 0 0 1 0 6 -3 0 9 6 6 3 9
|
inline |
This is the const version of topLeftCorner(Index, Index).
|
inline |
The template parameters CRows and CCols are the number of rows and columns in the corner.
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.topRightCorner<2,2>(): -5 -3 1 0 Now the matrix m is: 7 9 0 0 -2 -6 0 0 6 -3 0 9 6 6 3 9
|
inline |
This is the const version of topRightCorner<int, int>().
| cRows | the number of rows in the corner |
| cCols | the number of columns in the corner |
Example:
Output:
Here is the matrix m: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is m.topRightCorner(2, 2): -5 -3 1 0 Now the matrix m is: 7 9 0 0 -2 -6 0 0 6 -3 0 9 6 6 3 9
|
inline |
This is the const version of topRightCorner(Index, Index).
|
inline |
| N | the number of rows in the block |
Example:
Output:
Here is the array a: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is a.topRows<2>(): 7 9 -5 -3 -2 -6 1 0 Now the array a is: 0 0 0 0 0 0 0 0 6 -3 0 9 6 6 3 9
|
inline |
This is the const version of topRows<int>().
|
inline |
| n | the number of rows in the block |
Example:
Output:
Here is the array a: 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is a.topRows(2): 7 9 -5 -3 -2 -6 1 0 Now the array a is: 0 0 0 0 0 0 0 0 6 -3 0 9 6 6 3 9
References DenseBase().
|
inline |
This is the const version of topRows(Index).
References DenseBase().
|
inline |
Example:
Output:
Here is the matrix m: 7 6 -2 6 Here is the transpose of m: 7 -2 6 6 Here is the coefficient (1,0) in the transpose of m: 6 Let us overwrite this coefficient with the value 0. Now the matrix m is: 7 0 -2 6
Referenced by MatrixBase< Derived >::adjoint().
|
inline |
This is the const version of transpose().
Make sure you read the warning for transpose() !
|
inline |
This is the "in place" version of transpose(): it replaces *this by its own transpose. Thus, doing
has the same effect on m as doing
and is faster and also safer because in the latter line of code, forgetting the eval() results in a bug caused by aliasing.
Notice however that this method is only useful if you want to replace a matrix by its own transpose. If you just need the transpose of a matrix, use transpose().
*this must be a resizable matrix.
|
inline |
Referenced by bottomRows(), bottomRows(), Constant(), Constant(), Constant(), fill(), isApproxToConstant(), and middleRows().
| void visit | ( | Visitor & | visitor | ) | const |
Applies the visitor visitor to the whole coefficients of the matrix or vector.
The template parameter Visitor is the type of the visitor and provides the following interface:
References CoeffReadCost, and SizeAtCompileTime.
Referenced by maxCoeff(), maxCoeff(), minCoeff(), and minCoeff().
|
inlinestatic |
This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variants taking size arguments.
Example:
Output:
0 0 0 0 0 0 0 0
References Constant().
|
inlinestatic |
The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.
This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Zero() should be used instead.
Example:
Output:
0 0 0 0 0 0
References Constant().
|
inlinestatic |
The parameter size is the size of the returned vector. Must be compatible with this MatrixBase type.
This is only for vectors (either row-vectors or column-vectors), i.e. matrices which are known at compile-time to have either one row or one column.
This variant is meant to be used for dynamic-size vector types. For fixed-size types, it is redundant to pass size as argument, so Zero() should be used instead.
Example:
Output:
0 0 0 0 0 0
References Constant().
|
Outputs the matrix, to the given stream.
If you wish to print the matrix with a format different than the default, use DenseBase::format().
It is also possible to change the default format by defining EIGEN_DEFAULT_IO_FORMAT before including Eigen headers. If not defined, this will automatically be defined to Eigen::IOFormat(), that is the Eigen::IOFormat with default parameters.